Find Area Of A Circle With Circumference

As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. Given an object in real life having the shape of a circle, one approach might be to wrap a string exactly once around the object and then straighten the string and measure its length. Calculating areas and circumferences of circles plays an important role in almost all field of science and real life. For instance, formula for circumference and area of a circle can be applied into geometry. They are used to explore many other formulas and mathematical equations.

An arch length is a portion of the circumference of a circle. The ratio of the length of an arc to the circumference is equal to the ratio of the measure of the arc to $360$ degrees. A sector of a circles is the region bounded by two radii of the circle and their intercepted arc. Diameter is the line that separates the circle into two equal parts and is also equal to twice the radius. A circle is a fundamental shape that is measured in terms of its radius. In geometry or mathematics, a circle can be defined as a special variety of ellipse in which the eccentricity is zero and the two foci are coincident.

For any other value for the length of the radius of a circle, just supply a positive real number and click on the GENERATE WORK button. They can use these methods in order to determine the area and lengths of parts of a circle. The big \(A\) in the formulas is the area of the circle. This is the measure of how many square units, such as square centimeters or square inches, will fit inside the circle. If we wanted to paint a large solid circle as part of a mural, we'd need to know the area of the circle to calculate how much paint we would need to buy to fill in the whole circle.

The area of a circle formula is useful for measuring the region occupied by a circular field or a plot. Suppose, if you have a circular table, then the area formula will help us to know how much cloth is needed to cover it completely. The area formula will also help us to know the boundary length i.e., the circumference of the circle. A circle is a two-dimensional shape, it does not have volume. A circle only has an area and perimeter/circumference.

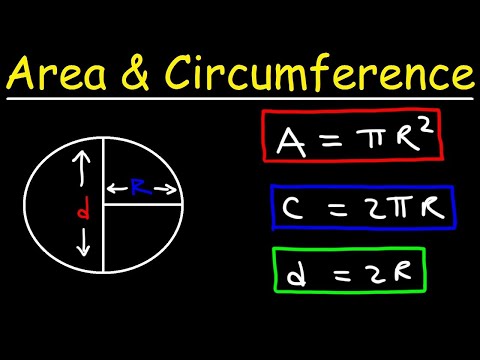
Let us learn in detail about the area of a circle, surface area, and its circumference with examples. The big \(C\) in the formulas is the circumference. It's like the perimeter of polygons and it's measured in length units like meters and feet.

If we were building a circular fence around a yard, you'd need to know the circumference of the circle to know how many feet of fence to buy. The area of the circle can be conveniently calculated either from the radius, diameter, or circumference of the circle. The constant used in the calculation of the area of a circle is pi, and it has a fractional numeric value of 22/7 or a decimal value of 3.14.

Any of the values of pi can be used based on the requirement and the need of the equations. The below table shows the list of formulae if we know the radius, the diameter, or the circumference of a circle. The diameter of a circle is twice to that of the radius. If the diameter or radius of a circle is given, then we can easily find the circumference. We can also find the diameter and radius of a circle if the circumference is given.

We round off to 3.14 in order to simplify our calculations. Circumference, diameter and radii are calculated in linear units, such as inches and centimeters. A circle has many different radii and many different diameters, and each one passes through the center. Remember that circumference and perimeter are alway measured in feet, inches, centimeters, etc. Area is alway measured in square units and volume always in cube units. Since area is a measure of two dimensions, you always report area in square units like square inches or square feet .

This is especially important when calculating the area of a circle for an assignment since an answer without correctly reported units is likely incorrect or incomplete. When the length of the radius or diameter or even the circumference of the circle is already given, then we can use the surface formula to find out the surface area. In technical terms, a circle is a locus of a point moving around a fixed point at a fixed distance away from the point. Basically, a circleis a closed curve with its outer line equidistant from the center.

The fixed distance from the point is the radius of the circle. In real life, you will get many examples of the circle such as a wheel, pizzas, a circular ground, etc. Now let us learn, what are the terms used in the case of a circle. To understand how to calculate circumference we must first begin with the definition of circumference. Circumference of a circle is linear distance around outer border of a circle. To find out the circumference, we need to know its diameter which is the length of its widest part.

The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . This concept can be of significance in geometry, to find the perimeter, area and volume of solids. Real life problems on circles involving arc length, sector of a circle, area and circumference are very common, so this concept can be of great importance of solving problems. In above program, we first take radius of circle as input from user and store it in variable radius.

Then we calculate the circumference of circle using above mentioned formulae and print it on screen using cout. For those having difficulty using formulas manually to find the area, circumference, radius and diameter of a circle, this circle calculator is just for you. The equations will be given below so you can see how the calculator obtains the values, but all you have to do is input the basic information. We have discussed till now the different parameters of the circle such as area, perimeter or circumference, radius and diameter. Let us solve some problems based on these formulas to understand the concept of area and perimeter in a better way. Fill the circle with radius r with concentric circles.

After cutting the circle along the indicated line in fig. 4 and spreading the lines, the result will be a triangle. The base of the triangle will be equal to the circumference of the circle, and its height will be equal to the radius of the circle. This area is the region that occupies the shape in a two-dimensional plane. Now we will learn about the area of the circle.

So the area covered by one complete cycle of the radius of the circle on a two-dimensional plane is the area of that circle. Now how can we calculate the area for any circular object or space? In this case, we use the formula for the circle's area. The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Today I am going to explain how to calculate the area and circumference of a circle using a class in TypeScript. Using this we can perform other types of calculations and generate the results.

I am going to discuss these axioms in a moment, but first let me show how Claim follows. But by Axiom 1 the length of the arc $PBQ$ is greater than $PQ$, while it follows from Euclid III.2 that $OB$ is greater than $OA$. Applying symmetry, this implies Claim in this case, and ought to suggest how the reasoning goes in general. Cover the circle with concentric circles of "r" radius. After dividing the circle along the designated line shown in the above figure and spreading the lines, the outcome will be a triangle. The base of the triangle will be equivalent to the circumference of the circle, and its height will be identical to the radius of the circle.

Below is the formula calculation for the same. When you are doing calculations involving a circle, you frequently use the number π, or pi. Pi is defined as being equal to the circumference of a circle -- the distance around that circle -- divided by its diameter. However, you don't need to memorize this formula when working with π, since it is a constant.

The perimeter of circle is nothing but the circumference, which is equal to twice of product of pi (π) and radius of circle, i.e., 2πr. The circle is divided into 16 equal sectors, and the sectors are arranged as shown in fig. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle.

Since the sectors have equal area, each sector will have an equal arc length. The red coloured sectors will contribute to half of the circumference, and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to πr and breadth equal to r. Hence, the concept of area as well as the perimeter is introduced in Maths, to figure out such scenarios. But, one common question that arises among most people is "does a circle have volume? Since a circle is a two-dimensional shape, it does not have volume.

In this article, let us discuss in detail the area of a circle, surface area and its circumference with examples. Finding the radius is not always easy, especially if you don't have the circle's center. You can calculate the area using the diameter instead.

The same formula applies as above, but you need first to calculate the radius of the circle. Simply divide the diameter by 2 to get the radius. In this method, we divide the circle into 16 equal sectors.

The sectors are arranged in such a way that they form a rectangle. All sectors are similar in area, so hence all sectors' arc length would be equal. The circle's area would be the same as the area of the parallelogram shape or rectangle. Only a mathematician can genuinely understand the practical importance of formulas for calculating area, radius, diameter, or circle circumference.

While most people think that formulas have no practical use, they are critical factors in many everyday life routines. The area of a circle is any space that the circle occupies on a flat surface. When we talk about the surface area of the circle, we are focusing on two-dimensional objects.

When finding the circle area, there are three other measures that we take into consideration, including the circumference, diameter, and radius. All three calculations also help us fining the circle area. Simply enter the desired value in the relevant box. Please use only numbers (e.g. enter 22 not 22 cm).

If you try to enter a unit of measure (e.g. 22 metres, 4 miles, 10 cm) you will get an NAN error appear in each box. When you have entered the number that you know, click the button on the right of that box to calculate all the other values. For example, if you know the volume of a sphere enter the value into the bottom box and then click the calculate button at bottom right. Not just this but there are some significant distances on a circle that needs to be calculated before finding the circumference of the circle. Diameter is the distance from one side of the circle to the other, crossing through the center/ middle of the circle.

A set of points in a plane equally distanced from a given point $O$ is a circle. The point $O$ is called the center of the circle. The distance from the center of a circle to any point on the circle is called the radius of this circle.A radius of a circle must be a positive real number. The circle with a center $O$ and a radius $r$ is denoted by $c$.

Area and circumference of circle calculator uses radius length of a circle, and calculates the perimeter and area of the circle. It is an online Geometry tool requires radius length of a circle. Using this calculator, we will understand methods of how to find the perimeter and area of a circle. The area of the circle formula can be used to calculate how much space a circular field or plot typically takes. If you have a plot and want to fence it, the area formula can help you figure out how much fencing you will need.

If you know the circumference, radius, or diameter of a circle, you can also find its area. Area represents the space enclosed within a circle. It's given in units of distance squared, such as cm2 or m2. The area is the measure of space confined within the boundary of a circle. The field within the boundary of the circle is the area utilized by the circle.

It may also be regarded as the total number of square units inside that circle. To recall, the area is the region that occupied the shape in a two-dimensional plane. In this article, you will learn the area of a circle and the formulas for calculating the area of a circle. The area of circle is the amount of two-dimensional space taken up by a circle.

Find Area Of A Circle Given Circumference We can calculate the area of a circle if you know its radius. The answer will be square units of the linear units, such as mm2, cm2, m2, square inches, square feet, and so on. Say you're trying to calculate the area of a circle with a radius of 3 inches. You would multiply 3 times 3 to get 9, and multiply 9 times π. Also note that when you multiply inches by inches, you get square inches, which is a measurement of area instead of length. Students beginning geometry can expect to encounter problem sets that involve calculating the area and circumference of a circle.

You can solve these problems as long as you know the circle's radius and can do some simple multiplication. If you learn the value of the constant π and the basic equations for a circle's properties, you can quickly find the area or circumference of any circle. As we know, the area of circle is equal to pi times square of its radius, i.e. π x r2. To find the area of circle we have to know the radius or diameter of the circle. A perimeter of closed figures is defined as the length of its boundary.